пʼятниця, 12 грудня 2014 р.
субота, 6 грудня 2014 р.
Застосування властивостей показникової функції
Узагальнення по темі показникова функція
Вправа 1
Презентація з теоретичним матеріалом
Вправа 2
Презентація із завданнями
Вправа 3
!!!!!Для домашнього опрацювання!!!!!
Вправа
Тести. Показникові рівняння та нерівності
Вправа 2
Залікова робота онлайн
Показникові рівняння
Вправа 1
Презентація з вправами
Вправа 2
Презентація з вправами продовження
Вправа 3
Вправа 4
Вправа
Вправа
Вправа
Вправа
пʼятниця, 5 грудня 2014 р.
Основні властивості логарифмів
Вправа 1
Логарифм числа. Властивості логарифмів (теорія)
Основні логарифмічні формули
Вправа 2
Вправа 3
Вправа 4
четвер, 4 грудня 2014 р.
Показникова функція
Вправа 1
Вправа 2
Вправа 3
Історична довідка
Термін "показник" для степеня ввів у 1553р. німецький математик (Спочатку монах, а потім- професор) Михайль Штифель (1487-1567).По-німецьки "показник"- Exponent, з латині exponere-"виставляти на показ"; exponens,exponentis "що виставляється на показ", "той, що показується".
Вправа 4
відео із сайту http://www.openclass.ru/node/475237
Розмноження бактерій
Колонія живих організмів (зокрема, бактерії) зростає в результаті розмноження. Якщо за рівні проміжки часу число живих організмів збільшується в одне й те саме число разів, то число N організмів по закінченні часу t після початку спостережень виражається формулою
N=N0 a kt, де a - постійна величина, що характеризує швидкість росту даної колонії, де а>1 це число залежить від біологічного виду організмів та від умов зовнішнього середовища.
Наприклад, для бактерії, що є збудником холери, число а близьке до 4.
Радіоактивний розпад
М= М 0 а k t - загальна формула, що характеризує радіоактивний розпад. Під час радіоактивного розпаду маса М речовини змінюється з плином часу t (років), М 0 - початкова маса речовин; k,а - постійні величини для цієї речовини.
Або: , якщо в початковий момент часу t0 Т - період напіврозпаду (проміжок часу, протягом якого початкова кількість речовин зменшується вдвічі). Наприклад, Т радію =1600 років, Т урану = 238 - 4,5 млрд років, Т цезію=137-31, Тйоду=8 діб
відео із сайту http://www.openclass.ru/node/475237
Розмноження бактерій
Колонія живих організмів (зокрема, бактерії) зростає в результаті розмноження. Якщо за рівні проміжки часу число живих організмів збільшується в одне й те саме число разів, то число N організмів по закінченні часу t після початку спостережень виражається формулою
N=N0 a kt, де a - постійна величина, що характеризує швидкість росту даної колонії, де а>1 це число залежить від біологічного виду організмів та від умов зовнішнього середовища.
Наприклад, для бактерії, що є збудником холери, число а близьке до 4.
Радіоактивний розпад
М= М 0 а k t - загальна формула, що характеризує радіоактивний розпад. Під час радіоактивного розпаду маса М речовини змінюється з плином часу t (років), М 0 - початкова маса речовин; k,а - постійні величини для цієї речовини.
Або: , якщо в початковий момент часу t0 Т - період напіврозпаду (проміжок часу, протягом якого початкова кількість речовин зменшується вдвічі). Наприклад, Т радію =1600 років, Т урану = 238 - 4,5 млрд років, Т цезію=137-31, Тйоду=8 діб
Вправа 5
Побудова графіків онлайн
Побудувати графіки функцій: y = 3^x;
y = 3^x - 2; y = 3^(x-2); y= - 3^x
Побудувати графіки функцій: y = 3^x;
y = 3^x - 2; y = 3^(x-2); y= - 3^x
Вправа 6
Побудувати графіки функцій: y = 2^x; y = 3^x;
чим більша основа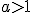 
, тим крутіше піднімається графік функції при русі точки зліво направо і тим швидше графік наближається до осі Ох при русі точки справа наліво.
Побудувати графіки функцій: y = (1/2)^x; y = (1/3)^x;
чим менша основа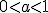 
, тим крутіше піднімається графік функції при русі точки справа наліво і тим швидше графік наближається до осі Ох при русі точки зліва направо.
!!!!!Для домашнього опрацювання!!!!!
!!!!!Для домашнього опрацювання!!!!!
Вправа
(рекомендовано спочатку завантажити на комп"ютер)
Презентація. Графік функції та завдання
Вправа
Вправа
Підписатися на:
Дописи (Atom)